Appearance
Manacher 算法可以在
例如
预处理
「奇数长度」和「偶数长度」的回文子串其实有区别。例如
在探测回文子串的长度时,我们采用「中心扩展法」,即确定中心并向两侧扩展,直到两端字符不同为止。
那么,针对「奇数长度」的回文子串,要以「字符」为中心扩展;针对「偶数长度」的回文子串,要以「字符间隙」为中心扩展。这意味着算法需要分别处理这两种情况,非常的麻烦。
并且,当回文子串扩展到字符串的开头和结尾时,需要额外的边界检查来防止数组越界。
Manacher 通过预处理来规避这些麻烦。
优化 1
Manacher 在字符间隙(包括字符串首尾)各插入一个特殊字符(如
优化 2
Manacher 在字符串的开头和结尾添加 不同 的特殊字符,这样一旦扩展到边界就会自动停止。
不得使用原字符串中存在的字符作为特殊字符。
原理
以下是一些变量的定义:
- 创建数组
,其中 表示以第 个字符为中心,能扩展的最大次数; 例如对
,以第 个字符 为中心,最多可向左右扩展 次,就记 。 - 使用两个变量
和 描述当前已知的最靠右的回文串的信息。 是其中心位置,初始为 ; 是其右边界位置,初始为 。
Manacher 算法的主要策略是:从左至右依次计算
假设当前要计算
Case 1:在 之内: 可以找到
关于 的对称点 。 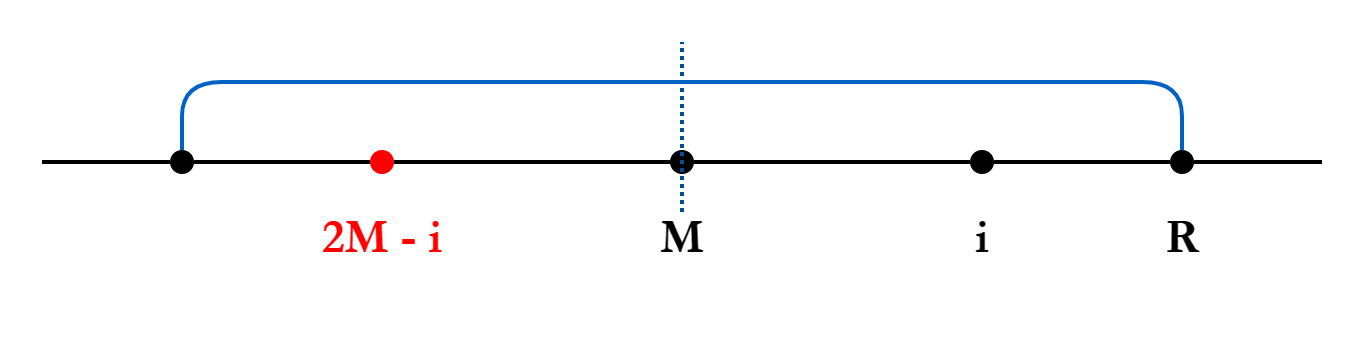
由于蓝色区域是一个回文串,我们可以通过其对称性获取一些信息。
Case 1.1:若: 我们知道
也是 到蓝区左端的距离。这种情况实际上是在说:以 为中心扩展,扩不出蓝区的范围。 由蓝区的对称性可知,以
为中心的「可扩展程度」和以 为中心的「可扩展程度」是相同的,于是有 。
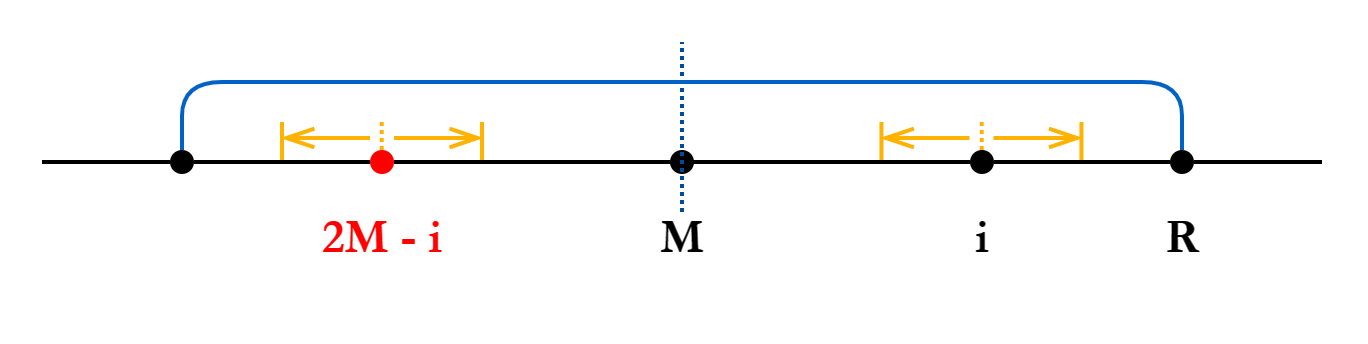
Case 1.2:若: 以
为中心扩展,可以扩展到蓝区外面。 由于蓝区以外的情况我们并不知晓,这种情况下
只能有一个 的保底。我们直接从 开始继续暴力扩展,从而得到 的实际值。 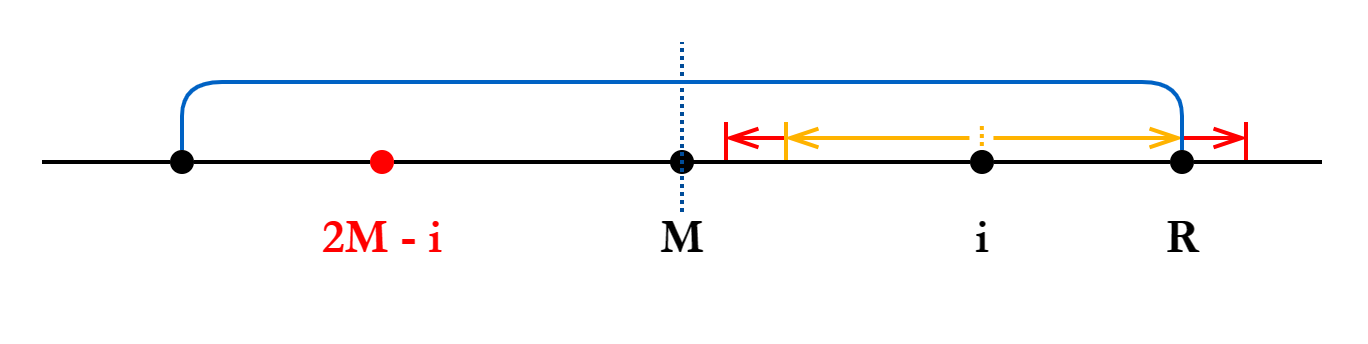
扩展完成后,我们得到了一个更靠右的回文串,需要相应地更新
和 的值。 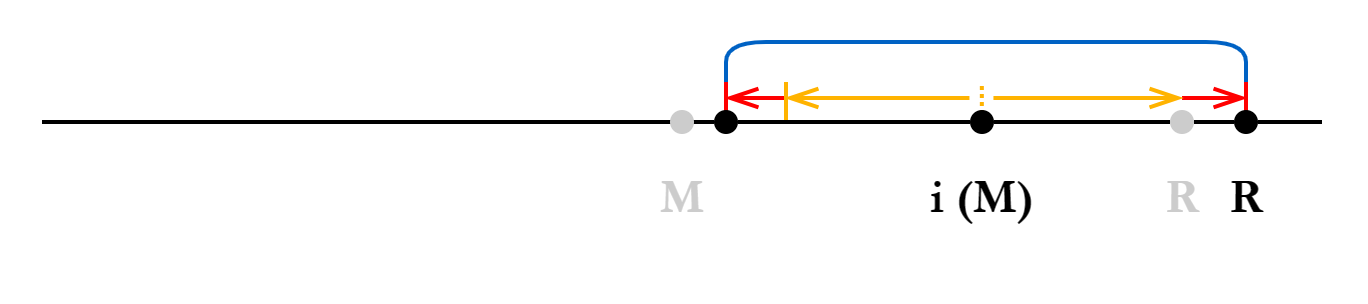
Case 2:在 之外: 这种情况就只能直接暴力扩展了。扩展完成后同样要更新
和 。 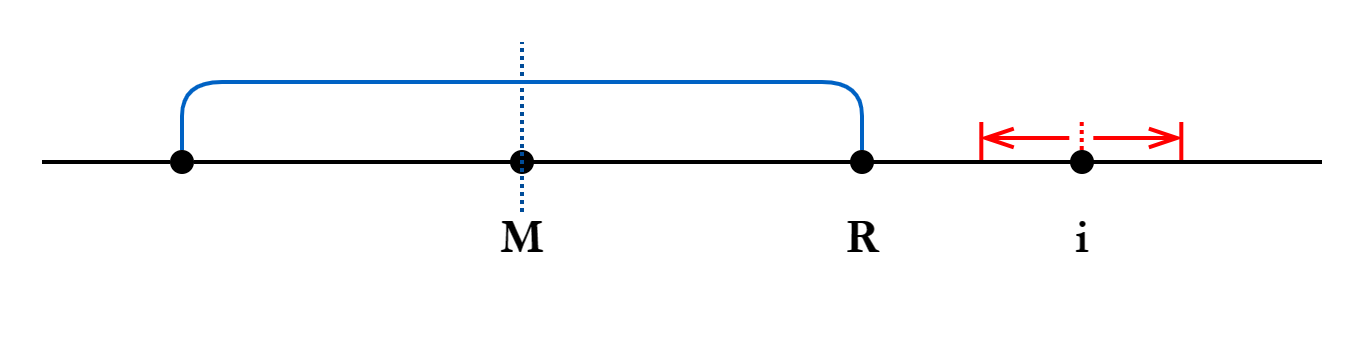
进一步简化算法的过程:
- 若
,则令 ; - 否则令
。
在此基础上,继续暴力扩展,得到
最后遍历数组
最后务必要把特殊字符去除掉。
每次暴力扩展的起点都是
模板
cpp
#include <bits/stdc++.h>
using namespace std;
string manacher(const string &s) {
string t = "@#";
for (char c : s) {
t += c;
t += "#";
}
t += '%';
vector<int> p(t.size());
int M = 0, R = 0;
for (int i = 1; i < t.size() - 1; i ++) {
p[i] = (i > R) ? 0 : min(p[2 * M - i], R - i);
while (t[i + p[i] + 1] == t[i - p[i] - 1])
p[i] ++;
if (i + p[i] > R) {
M = i;
R = i + p[i];
}
}
int maxM = 0, maxP = 0;
for (int i = 1; i < t.size() - 1; i ++) {
if (p[i] > maxP) {
maxM = i;
maxP = p[i];
}
}
int start = (maxM - maxP) / 2;
return s.substr(start, maxP);
}
int main() {
string s;
cin >> s;
cout << manacher(s) << endl;
return 0;
}回文串是指正读和反读都相同的字符串。 ↩︎