简介

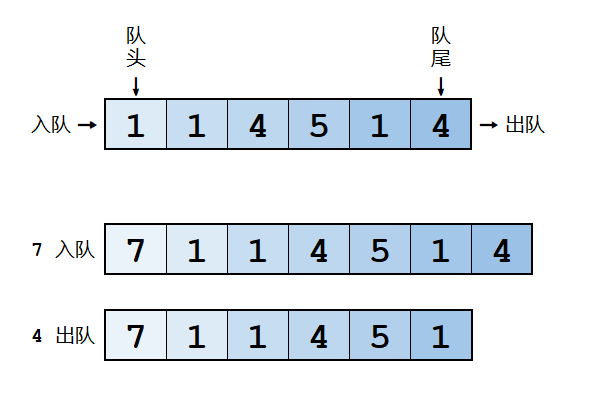
队列是一种「先进先出」的数据结构。元素从队列的前端进入（入队），从末端离开（出队），类似于排队。

双向队列

双向队列支持从两端插入或删除元素。

单调队列

单调队列的元素从队头到队尾满足单调性，适用于查询某一动态区间的最大（或最小）元素。

单调队列一般使用 双向队列 实现。

插入元素

将 $A[i]$ 入队时，需要维护队列单调性，同时保证队列元素在 $A[p\cdots i]$ 范围内。

以单调递增队列为例，维护操作如下：

1. 重复弹出队头，直到队头 $\ge p$；
2. 重复弹出队尾，直到 $A[$队尾$]<A[i]$；
3. 将 $i$ 入队。

此时 $A[p\cdots i]$ 范围内最小元素为 $A[$队头$]$。

TIP

这里的单调队列中，存储的是下标值。队列内元素按 $A$ 的值单调递增。

deque<int> q; // 存储元素下标

void insert(int i, int p) { // 将 a[i] 入队，维护队列元素在 a[p...i] 范围内
    while (!q.empty() && q.front() < p)
        q.pop_front();
    while (!q.empty() && a[q.back()] >= a[i])
        q.pop_back();
    q.push_back(i);
}

滑动窗口

一个滑动窗口（长度为 $k$）从数组 $A$ （长度为 $n$）的左端移动到右端，每次只向右移一位。求每次滑动时窗口区中的最大值。

示例（$k=3,n=8$，红色数值在窗口区内）：

$A_1$	$A_2$	$A_3$	$A_4$	$A_5$	$A_6$	$A_7$	$A_8$	最大值
			-3	5	3	6	7	3
1				5	3	6	7	3
1	3				3	6	7	5
1	3	-1				6	7	5
1	3	-1	-3				7	6
1	3	-1	-3	5				7

朴素算法

枚举 $i=k\to n$，顺序地查找 $A[i-k+1\cdots i]$ 中的最大整数。

时间复杂度为 $O(nk)$。

for (int i = k; i <= n; i ++) {
    int maxn = a[i];
    for (int j = i - k + 1; j <= i; j ++)
        maxn = max(maxn, a[j]);
    cout << maxn << ' ';
}

单调队列优化

使用单调递减队列优化「查找 $A[i-k+1\cdots i]$ 中的最大整数」的效率。

时间复杂度为 $O(n)$。

deque<int> q;

void insert(int i, int p) {
    while (!q.empty() && q.front() < p)
        q.pop_front();
    while (!q.empty() && a[q.back()] <= a[i])
        q.pop_back();
    q.push_back(i);
}

for (int i = 1; i <= n; i ++) {
    insert(i, i - k + 1);
    if (i >= k)
        cout << a[q.front()] << ' ';
}